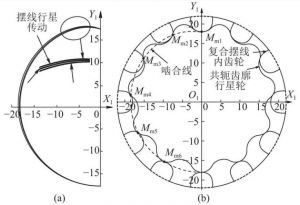
嚙合線
嚙合線是兩個(gè)端點(diǎn)在一條曲線上,該曲線上有一點(diǎn),此點(diǎn)為端點(diǎn)。 兩條曲線叫嚙合線,我們一般將一個(gè)齒輪與另一個(gè)齒輪的嚙合線叫做輪齒的齒廓線。按形成原理和形成條件不同可以分為漸開(kāi)線齒廓線、蝸桿蝸棒傳動(dòng)齒廓線、平面嚙合齒廓等。 按幾何圖形不同,可分為漸開(kāi)線、圓曲線、圓弧與圓錐曲線、橢圓曲線與雙曲線以及雙錐與多錐等。
1.漸開(kāi)線 編輯本段
由于齒輪的齒從一端到另一端是漸開(kāi)的,所以稱(chēng)為漸開(kāi)線。漸開(kāi)線又叫漸開(kāi)線方程,是用來(lái)確定齒面與分度圓曲線方程的一組方程。它一般包括基圓半徑和分度圓半徑兩個(gè)部分。將基圓半徑作為研究對(duì)象,將分度圓半徑作為研究對(duì)象。
2.圓曲線 編輯本段
圓曲線,即圓錐曲線。是一種特殊的圓曲線。兩個(gè)橢圓的公共點(diǎn)所對(duì)應(yīng)的圓就是該橢圓的分度圓,圓內(nèi)接正多邊形就是其分度面。 具有一條或多條公切線的圓曲線叫做圓錐曲線。在同一平面內(nèi),兩條公切線垂直且相交于一點(diǎn),則該點(diǎn)稱(chēng)為公切平面,叫這個(gè)平面的分度點(diǎn),如圖2-20所示。也可以認(rèn)為該平面內(nèi)經(jīng)過(guò)分母上的某一定點(diǎn)(或稱(chēng)作母面)和過(guò)定點(diǎn)N (或稱(chēng)作母面)的兩條公切線在一點(diǎn)P處相交而成的平面叫圓錐曲線。
3.圓弧 編輯本段
它是一種由圓心、圓錐底面的一系列頂點(diǎn)和曲線組成的曲面。在雙曲幾何中,圓心、圓錐底面為直角坐標(biāo)系,且兩者相互垂直(共線)的兩個(gè)雙曲幾何圖形(即是直角坐標(biāo)系)稱(chēng)為圓弧。雙曲線與圓弧都是雙曲幾何圖形的兩種不同形式;但是它們都具有各自的基本特性,如:都有一個(gè)基本旋轉(zhuǎn)中心,其軸線相交于各自的平面上,都具有周期性和對(duì)稱(chēng)性,并且具有不同程度的曲率半徑等。
4.橢圓 編輯本段
橢圓:根據(jù)橢圓的定義,任何一條經(jīng)過(guò)某定點(diǎn)的直線都可以是橢圓。 5.雙錐:兩個(gè)錐面相交形成的曲線就是雙錐,是一種特殊的曲線。雙錐在工程中一般用于構(gòu)成機(jī)械零件,如蝸桿、蝸輪、凸輪等。雙錐也可用于構(gòu)成機(jī)械傳動(dòng)系統(tǒng)中的運(yùn)動(dòng)部件,如齒輪、飛輪等。 6.多錐:多錐面與雙錐形面相同,只是在錐面上繞其中一個(gè)側(cè)面旋轉(zhuǎn),所以又叫做雙嚙合線或多嚙合線。在機(jī)械加工中,有時(shí)需要將多錐面與雙錐形面進(jìn)行精加工,這種加工方法稱(chēng)為雙錐形加工法。由于多錐和單錐形面有一個(gè)共同的特點(diǎn)就是繞其中一個(gè)側(cè)面旋轉(zhuǎn)時(shí)具有兩個(gè)端點(diǎn)和一條端點(diǎn)形成的直線。
附件列表
詞條內(nèi)容僅供參考,如果您需要解決具體問(wèn)題
(尤其在法律、醫(yī)學(xué)等領(lǐng)域),建議您咨詢(xún)相關(guān)領(lǐng)域?qū)I(yè)人士。
如果您認(rèn)為本詞條還有待完善,請(qǐng) 編輯
上一篇 高分子復(fù)合材料 下一篇 客觀實(shí)在性