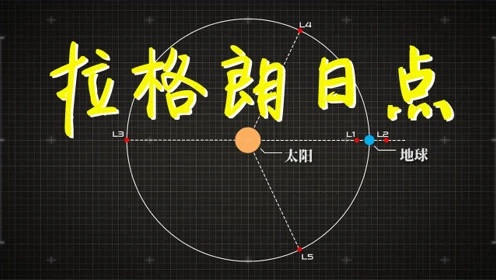
拉格朗日點(diǎn)（Lagrange   points）它是天體力學(xué)中平面圓受限三體的五個(gè)特解。又被稱為平動(dòng)點(diǎn)。小質(zhì)量的天體(忽略為質(zhì)點(diǎn))空間中的一點(diǎn)，在兩個(gè)大質(zhì)量天體的引力作用下，一個(gè)小物體相對(duì)于兩個(gè)大物體保持基本靜止。

在每個(gè)由兩個(gè)大質(zhì)量天體組成的系統(tǒng)中，推斷有五個(gè)拉格朗日點(diǎn)，其中兩個(gè)是穩(wěn)定解，即在受到外力后趨于回到原來的相對(duì)位置。1767年，瑞士數(shù)學(xué)家萊昂哈德·歐拉（Leonhard   Euler）計(jì)算前三個(gè)拉格朗日點(diǎn)。法國著名數(shù)學(xué)家、物理學(xué)家約瑟夫·路易斯·拉格朗日（Joseph-地址Louis Lagrange）1772年，推斷出還剩兩個(gè)。后來，這五個(gè)點(diǎn)被稱為“拉格朗日點(diǎn)”。

到2023年，拉格朗日點(diǎn)的小天體相對(duì)于大天體是相對(duì)靜止的，這在天文學(xué)中已經(jīng)得到了廣泛的應(yīng)用、航空航天等領(lǐng)域。例如，著名的詹姆斯·韋伯太空望遠(yuǎn)鏡被設(shè)置在這一天-論地球系統(tǒng)中的拉格朗日點(diǎn)。

發(fā)現(xiàn)

上述三體運(yùn)動(dòng)中求解小天體位置的問題也叫“平面圓形受限三體”當(dāng)小天體的質(zhì)量可以忽略時(shí)，這個(gè)問題有五種特殊解法。1767年，瑞士數(shù)學(xué)家萊昂哈德·歐拉（Leonhard   Euler）根據(jù)旋轉(zhuǎn)的兩體引力場(chǎng)，計(jì)算出三個(gè)特解，這三點(diǎn)后來被稱為L(zhǎng)1、L2和L3，五年后，法國數(shù)學(xué)家約瑟夫·路易·拉格朗日（Joseph-地址Louis Lagrange）計(jì)算剩下的兩個(gè)特解L4和L5。后來人們把這五個(gè)點(diǎn)統(tǒng)稱為拉格朗日點(diǎn)。

證實(shí)

拉格朗日點(diǎn)在1906年首次被證明，這一年天文學(xué)家馬克斯·沃爾夫（Max Wolf）在火星和木星之間的主帶外發(fā)現(xiàn)了一顆小行星。它圍繞太陽的軌道與木星完全相同它在木星前面運(yùn)行。似乎這顆小行星-木星-太陽始終位于一個(gè)等邊三角形的三個(gè)頂點(diǎn)上，這顆小行星就是以特洛伊戰(zhàn)爭(zhēng)中的人物命名的“阿基里斯”同年，天文學(xué)家發(fā)現(xiàn)木星上出現(xiàn)了一顆名為617的小行星s軌道這顆小行星運(yùn)行在木星后面，木星后面60度。這顆小行星也與木星和太陽形成等邊三角形。

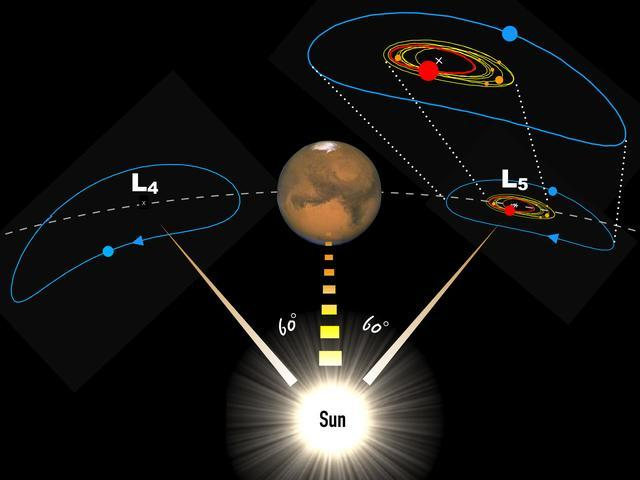
20世紀(jì)80年代，科學(xué)家在土星及其大型衛(wèi)星組成的運(yùn)動(dòng)系統(tǒng)中發(fā)現(xiàn)了類似的等邊三角形。到2009年，天文學(xué)家已經(jīng)在木星的L4和L5周圍發(fā)現(xiàn)了1000多顆小行星。兩個(gè)拉格朗日點(diǎn)L4和L5也稱為三角形拉格朗日點(diǎn)或特洛伊點(diǎn)。這些事實(shí)無可辯駁地證明了拉格朗日點(diǎn)的存在和正確性。

拉格朗日點(diǎn)的穩(wěn)定性

不穩(wěn)定拉格朗日點(diǎn)（L1、L2和L3）

在這五個(gè)拉格朗日點(diǎn)中，有三個(gè)不穩(wěn)定的拉格朗日點(diǎn)，即L1、L2和L3位于兩個(gè)大質(zhì)量天體的連線上，也稱為共線平移點(diǎn)。L1對(duì)應(yīng)的是兩個(gè)大天體引力之差提供一個(gè)小天體繞質(zhì)心圓周運(yùn)動(dòng)的情況，L2和L3對(duì)應(yīng)的是兩個(gè)大天體引力之和提供一個(gè)小天體繞質(zhì)心圓周運(yùn)動(dòng)的情況。通過數(shù)學(xué)計(jì)算發(fā)現(xiàn)，當(dāng)質(zhì)量參數(shù)μ變化時(shí)，共線平移點(diǎn)的位置也會(huì)發(fā)生變化下圖顯示了不同質(zhì)量參數(shù)下共線平移點(diǎn)的位置變化虛線代表兩個(gè)大天體的位置，縱坐標(biāo)是兩個(gè)主天體之間的距離。通過對(duì)圖像的分析，我們可以知道這三個(gè)拉格朗日點(diǎn)是不穩(wěn)定的拉格朗日點(diǎn)，這些點(diǎn)上的小天體可能會(huì)因?yàn)閿_動(dòng)而偏離軌道。

穩(wěn)定拉格朗日點(diǎn)（L4和L5）

對(duì)于L4和L5，無論質(zhì)量參數(shù)如何變化，這兩個(gè)拉格朗日點(diǎn)和兩個(gè)大天體始終保持等邊三角形構(gòu)型，因此非常穩(wěn)定，這兩個(gè)點(diǎn)上的行星不容易發(fā)生位移這兩個(gè)點(diǎn)也稱為三角形平移點(diǎn)。

探測(cè)

尋找拉格朗日點(diǎn)最直觀的方法就是通過有效勢(shì)能推導(dǎo)出物體的力。等勢(shì)線最密的地方力最強(qiáng)，等勢(shì)線稀疏的地方力最弱。如下圖所示，高點(diǎn)為黃色，低點(diǎn)為紫色通過這種分析方法，可以快速分析出拉格朗日點(diǎn)的位置。

對(duì)于人類來說，不同的拉格朗日點(diǎn)有不同的應(yīng)用，最重要的拉格朗日點(diǎn)就是地球-太陽系統(tǒng)和月球-地球系統(tǒng)中的拉格朗日點(diǎn)。

地球-太陽系統(tǒng)

共線平動(dòng)點(diǎn)

由于共線平動(dòng)點(diǎn)處的不穩(wěn)定性，在共線平動(dòng)點(diǎn)附近沒有自然天體長(zhǎng)期運(yùn)行，所以地球-太陽系的共線平動(dòng)點(diǎn)L1相對(duì)于太陽和地球具有相對(duì)固定的幾何構(gòu)型，可以提供不間斷的太陽視野，因此在日地關(guān)系的觀測(cè)中有著非常重要的應(yīng)用。例如，太陽和L2點(diǎn)在今天有非常重要的應(yīng)用由于其非常穩(wěn)定的熱力學(xué)環(huán)境和相對(duì)固定的與地球的配置，美國的天文觀測(cè)任務(wù)。例如，著名的詹姆斯·韋伯太空望遠(yuǎn)鏡被設(shè)置在這一天-地球系統(tǒng)中的L2拉格朗日點(diǎn)。此外，L2也是普朗克和WMAP的所在地。至于L3，截至2023年，天文學(xué)家還沒有發(fā)現(xiàn)任何用處，因?yàn)樗冀K在太陽后面，那里的航天器很難與地球建立穩(wěn)定的通信系統(tǒng)。但是隱藏星球L3的想法一直是科幻寫作的熱門話題。

截至2023年，日本已被全球訪問-地球系統(tǒng)共線平移點(diǎn)的任務(wù)如下：ISEE-3/ICE、WIND、SOHO、ACE、DSCOVER、LPF、WMAP、GENESIS、Uranus、PLANCK、GAIA、嫦娥二號(hào)等。

月球-地球系統(tǒng)

共線平動(dòng)點(diǎn)

月球-地球系統(tǒng)的共線平動(dòng)點(diǎn)L1與地球和月球的幾何構(gòu)型幾乎相同，未來可以作為地球使用-月轉(zhuǎn)移的中繼點(diǎn)。由于L2附近的軌道可以連續(xù)觀測(cè)月球背面，與地球的通信不受月球阻擋，因此可以作為月球背面與地球觀測(cè)站的中繼通信。例如我國“鵲橋中繼衛(wèi)星”在繞地球旋轉(zhuǎn)的同時(shí)繞著拉格朗日點(diǎn)L2旋轉(zhuǎn)，“鵲橋中繼衛(wèi)星”它可以作為中繼站，將月球背面探測(cè)器發(fā)射的信號(hào)無障礙地傳輸?shù)降厍颉?/p>

2015年，中國 美國的宇宙飛船第一次到達(dá)地面-月L2點(diǎn)。到2023年，全世界都去過月球-地球系統(tǒng)共線平移點(diǎn)的任務(wù)如下：ARTEMIS、GRAIL、CE5/T1等。

三角平動(dòng)點(diǎn)

截至2023年，相關(guān)學(xué)者已在現(xiàn)場(chǎng)-月球系統(tǒng)的三角形平移點(diǎn)的應(yīng)用已經(jīng)在理論上進(jìn)行了研究，但日本探測(cè)器天妃除外，該探測(cè)器于1990年代飛越地球-除了三角平動(dòng)點(diǎn)之外，沒有與月球系統(tǒng)相關(guān)的空間任務(wù)。